Statistical mechanics in biology and biocomputation
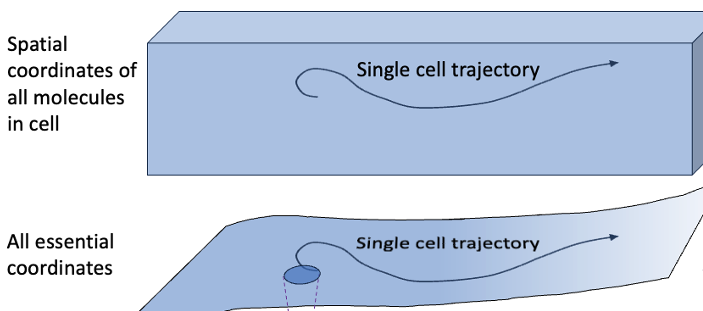
So you know about molecular biophysics and want to think about cells. How should you get started? Let’s take the first few steps.
We’ll start with some concepts that should be familiar: coordinates and equilibrium vs. nonequilibrium behavior. We can frame our discussion by comparing something familiar, a protein, to a cell.
Continue reading
Although I like to think of myself as a reader-oriented science writer, there seems to be something innate in me that doesn’t always put the reader first.
Continue reading
When we want to estimate parameters from data (e.g., from binding, kinetics, or electrophysiology experiments), there are two tasks: (i) estimate the most likely values, and (ii) equally importantly, estimate the uncertainty in those values. After all, if the uncertainty is huge, it’s hard to say we really know the parameters. We also need to choose the model in the first place, which is an extremely important task, but that is beyond the scope of this discussion.
Continue reading
I think self-confidence is an essential ingredient of doing well in science, but it’s not discussed enough. I have thought about confidence a lot because I don’t always have it. I’m over 50 years old and have published plenty of papers, but often enough I doubt myself. I have this intermittent, but deep-seated worry that maybe my science isn’t so great. Sometimes I get pretty nervous before giving a talk (which I do my best to hide) even though I enjoy lecturing. This long-lived impostor syndrome is frustrating, but it’s part of who I am.
Continue reading
Markov state models (MSMs) are very popular and have a rigorous basis in principle, but applying them in practice must be done with great caution. There is no guarantee the results will be reliable for complex systems of typical interest unless there is an enormous amount of data and significant expertise and validation goes into the MSM building. And even if those conditions are in place, certain observables likely will be biased.
Continue reading
Count me among the weak of science.
Here I am again, feeling defensive, irate at reviewer critiques of our recent sub-Nobel prize work. Only in this case, the reviews are in my mind, yet to arrive. In fact, we haven’t even drafted the paper yet! But I can foresee what will happen. After all, if I’m honest, our contribution is clearly incremental.
Is it a failure? Were my expectations way off, again?
Continue reading
Many scientists say they dislike writing, but I want to persuade you not to be one of them. Writing not only is the way to convince folks how important your work is, but it can be a key part of doing good science in the first place. Your work must be explainable in a concise and logical way … or else it may not be logical!
And writing can be fun, once you realize it’s another more-or-less scientific puzzle to solve: how to explain what you’re doing to a target audience (or audiences). What’s the one-sentence version of your work? The three-sentence version? How would these change for more general or more technical audiences?
Continue reading
Did you know that you can significantly change women’s performance on a challenging math test simply by providing a different explanation of the purpose of the test up front? And the same for Black students? Did you know there are ways to give advice and feedback that are demonstrated to improve performance in groups that suffer from (unconscious but inevitable) internalization of stereotypes? I learned these facts just a few weeks ago and find them astonishing. How can these crazy but simple things be true, and more importantly, why don’t most of us – professional scientists – know about them?
The key lesson of all these exercises is that you can push yourself to be better and more confident in theory by tackling simple, paradigmatic problems in an incremental way. You must put pencil to paper! You must do it regularly. But once you do, the benefits come quickly. Each mini-realization builds into knowledge. Each solved simple problem builds your intuition for understanding complex systems.
Give yourself a pat on the back if you’ve come this far. You have used simple exact solutions to differential equations to grasp the essentials of non-equilibrium processes. But there’s the physical process on the one hand, and the mathematical description on the other. We’ve used continuous-time math thus far. We now move to discrete time and get a taste for “Markov state models,” which implicitly employ time discretization in the field of biomolecular simulation.