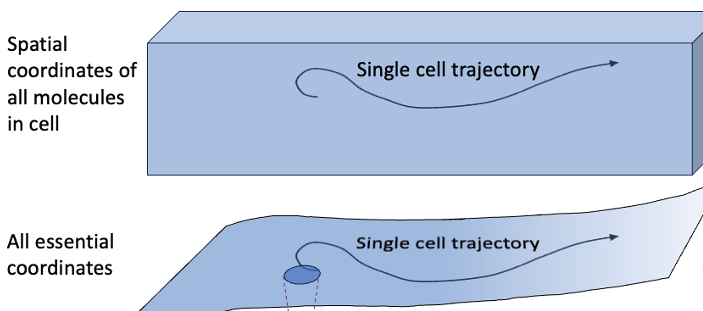
The Markov model, without question, is one of the most powerful and elegant tools available in many fields of biological modeling and beyond. In my world of molecular simulation, Markov models have provided analyses more insightful than would be possible with direct simulation alone. And I’m a user, too. Markov models, in their chemical-kinetics guise, play a prominent role in illustrating cellular biophysics in my online book, Physical Lens on the Cell.
Yet it’s fair to say that everything is Markovian and nothing is Markovian – and we need to understand this.
If you’re new to the business, a quick word on what “Markovian” means. A Markov process is a stochastic process where the future (i.e., the distribution of future outcomes) depends only on the present state of the system. Good examples would be chemical kinetics models with transition probabilities governed by rate constants or simple Monte Carlo simulation (a.k.a. Markov-chain Monte Carlo). To determine the next state of the system, we don’t care about the past: only the present state matters.
Continue reading



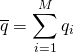 . We can also calculate the standard deviation σ of these values in the usual way as the square root of the variance. Both of these quantities will approach their “true” values (based on the simulation protocol) with enough sampling – with large enough
. We can also calculate the standard deviation σ of these values in the usual way as the square root of the variance. Both of these quantities will approach their “true” values (based on the simulation protocol) with enough sampling – with large enough 



