Three states – now that is exciting! And I’m not kidding. You are poised to understand critical timescales in non-equilibrium statistical mechanics.

We have been studying the linear three-state system.

C:\Users\zuckermd\Box\physicalLens\htmlPhysicalLens\images\discreteThreeStateLinear.png

Let’s quickly go over the answers from last time.

  1. Write down the ODEs for this system.

    1. These are a straightforward generalization of the two-state case:

      (1)   \begin{align*} \frac{ d P_1 }{ dt } &= - P_1 k_{12} + P_2 k_{21} \\ \frac{ d P_2 }{ dt } &= - P_2 (k_{21}+k_{23}) + P_1 k_{12} + P_3 k_{32} \\ \frac{ d P_3 }{ dt } &= - P_3 k_{32} + P_2 k_{23} \end{align*}

  2. Solve for the equilibrium populations of this system.

    1. These can be determined “by inspection” as people more experienced than you always said in a most annoying way. Well, you could solve the detailed balance equations (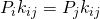P_i k_{ij} = P_j k_{ij}) along with the probability normalization condition (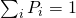\sum_i P_i = 1). Or for, say 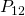P_{12}, you could ask: what fraction can be multiplied by the outgoing rate k_{12} so that it has to balance the incoming probability flow from state 2? That’s the “by inspection” strategy. Stare at these for a while and you’ll see they have to be correct.

          \[P^{eq}_1 = \frac{k_{21} k_{32}}{\Sigma} \hspace{1cm} P^{eq}_2 = \frac{k_{12} k_{32}}{\Sigma} \hspace{1cm} P^{eq}_3 = \frac{k_{13} k_{12}}{\Sigma}\]

      Here, \Sigma is the sum of the numerators to ensure normalization.

  3. Sketch and write down the ODEs for a non-equilibrium steady state in which transition events from state 2 to 3 immediately generate feedback to state 1. That is, no transitions from 3 to 2 are allowed (so 3 can be called an absorbing state) and transitions from 2 to 3 effectively become transitions from 2 to 1 (though governed by the 2-to-3 rate constant).

    1. Here’s a sketch.
      C:\Users\zuckermd\Box\physicalLens\htmlPhysicalLens\images\discreteThreeStateFeedback.png
      And here are the ODEs:

      (2)   \begin{align*}\frac{ d P_1 }{ dt } &= - P_1 k_{12} + P_2 (k_{21} + k_{23}) \\\frac{ d P_2 }{ dt } &= - P_2 (k_{21} + k_{23}) + P_1 k_{12} \end{align*}

      As intended, the flow from state 2 to 3 has been diverted (or ‘recycled’ or ‘fed back’) to state 1. State 3 is an absorber which directly feeds state 1.

Did you see what we did? The set of equations (2) have just two states, because P_3=0 for all times by our assumption that probability that reaches state 3 immediately gets fed to state 1.

Now you can do some more simple math and learn a lot, really a lot. I’m not kidding – this is going to be HUGE! Here are the new questions, with more to come next time to complete your understanding. We are still roughly following along with material from my website, so please cheat! But remember to force yourself to do the exercises from scratch the next day.

  1. Write down the exact solution to the set of ODEs (2). No math is required at all. Instead, use the solutions you already know for the two-state system, and just substitute in the rates.
  2. What is the new relaxation time (time constant of the exponential)? Does the (algebraic) dependence of this timescale on the various rate constants make sense?
  3. As t \to \infty, the system does not relax to equilibrium. Find the t \to \infty state probabilities and show that detailed balance does not hold – at least in the usual sense. That is, show that P_1(t\!\to\!\infty) k_{12} \neq P_2(t\!\to\!\infty) k_{21}.
  4. Instead the system relaxes to a non-equilibrium steady state. Describe in words the basic property of any steady state and show that the steady probabilities satisfy this property for both states.
  5. Remind yourself that equilibrium is a special steady state. Explain why detailed balance implies steady state, but note that our system shows the reverse is not true in general.