The key lesson of all these exercises is that you can push yourself to be better and more confident in theory by tackling simple, paradigmatic problems in an incremental way. You must put pencil to paper! You must do it regularly. But once you do, the benefits come quickly. Each mini-realization builds into knowledge. Each solved simple problem builds your intuition for understanding complex systems.
Below are solutions to the problems from last time. Looking for more? Scroll down for some additional problems.
Here are the answers to the questions from last time, which explain the connection between continuous and discrete-time kinetic descriptions.
-
Give the full definition of
 and explain why it’s dimensionless.
and explain why it’s dimensionless.
-
This is the conditional to probability to be in state
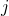 at time
at time  if a system was in state
if a system was in state 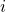 at time
at time 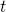 . Importantly, it’s completely irrelevant to
. Importantly, it’s completely irrelevant to  where the system may have been in between
where the system may have been in between 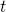 and
and  . It only matters where the system is at the times we’re “looking.” The probability
. It only matters where the system is at the times we’re “looking.” The probability  is dimensionless because it’s simply a probability – the fractional chance to be in state
is dimensionless because it’s simply a probability – the fractional chance to be in state 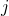 – and not a probability per unit time like a rate constant.
– and not a probability per unit time like a rate constant.
-
This is the conditional to probability to be in state
-
If
 is the time-dependent probability of state
is the time-dependent probability of state 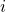 , show that
, show that  .
.
-
At time
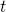 , some fraction of the probability is in each state
, some fraction of the probability is in each state 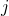 , including
, including  . Then the total probability in state
. Then the total probability in state 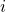 at the later time
at the later time  is the sum of the ‘contributions’ to state
is the sum of the ‘contributions’ to state 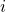 from every state indexed by
from every state indexed by 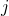 (including
(including  ) based on the
) based on the  . More precisely,
. More precisely,  is the fraction of the state
is the fraction of the state 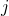 probability which ends up in
probability which ends up in 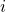 , implying
, implying 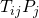 is the fraction ‘contributed’.
is the fraction ‘contributed’.
-
At time
-
Using the exact solutions to the continuous-time two-state probabilities,
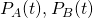 , which we derived previously, calculate the discrete-time transition probabilities
, which we derived previously, calculate the discrete-time transition probabilities 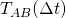 and
and  for transitions into state A. This problem is trickier than it sounds (though the math is easy), but don’t worry the derivation is there for you in the notes. The key trick is to write
for transitions into state A. This problem is trickier than it sounds (though the math is easy), but don’t worry the derivation is there for you in the notes. The key trick is to write  in terms of
in terms of 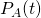 and
and 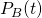 using the fact that
using the fact that  for any/all
for any/all 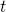 .
.
- For this, please just look at the notes. It’s written out carefully there.
Going forward, here are some key problems you should solve.
- Demonstrate the correctness of the (differential) continuity equation in one dimension by integrating the probability over a small increment.
- Derive the diffusion equation via a Taylor expansion of the time-varying probability distribution. See my online notes.
- Derive the Smoluchowski equation via a Taylor expansion of the time-varying probability distribution. See my online notes.
- Show that the stationary distribution of the Smoluchowski equation is the Boltzmann distribution.
- Show that overdamped dynamics lead to the Boltzmann distribution. For hints, see Sec. IIB of this paper by Chandler’s group.
- Derive the replica-exchange Metropolis acceptance criterion. For hints, see Ch. 12 of my textbook.
- Explain why one takes a linear average of MD or MC snapshots (equally spaced in time) to obtain a Boltzmann-weighted average. See Ch. 2 of my textbook.
- Derive the ideal gas partition function from scratch. See Ch. 5 of my textbook.
Good luck! Work hard, but work slow …

