With this post I want to begin a series of exercises designed to grow your strength in theory pertinent to statistical biophysics – i.e., in math, physics, theoretical chemistry. The goal is to help you find a sweet spot where you push yourself a little bit, and regularly so you can continue to improve. Along the way, you’ll (re)learn critical statistical physics, which will help you understand, implement, and assess methods and findings more effectively. Of course, you’re in!
OK, some of you may be skeptical. We all know someone smarter, more knowledgeable, faster on their feet. It’s intimidating to interact with such people. (Yes, for me too.) Every one of us has tried and utterly failed to understand some technical paper we thought was important to our work. Should we declare ourselves inadequate and give up?
No, we must continue to make an effort to improve in theory. If we stop making the effort, that’s when we really waste our potential as thinkers. We may not have the time or patience to take classes, but we can still make a systematic effort.
Let me “prove” to you that you can learn additional technical material. My basic claim is that your theory strength is mostly an issue of knowledge, not ability. There’s a saying that “math is locally trivial,” (though I don’t find a good source – let me know if you know one). I firmly believe this. Each step is simple, once you understand the right steps to take. And this can be learned. Think of something you know really well, perhaps calculus in one dimension, or maybe simple algebra. If you interact with a student of reasonable ability, but no knowledge of your area of expertise, that student probably will think you’re smarter. Is that true, or do you just know the steps and have experience?
The most important thing is to stay in the habit of pushing yourself to understand at least a little bit more on a regular basis.
Besides the knowledge and understanding, what’s the value of understanding theory better? The key is that it helps you set things in context. That new paper claiming a dramatic result – could it possibly be true? The other paper with a super-complicated title – could it just be a small twist on something you know? As theoretical scientists, we don’t want to take others at their word. We want to learn from their successes and failures to make our efforts more fruitful.
What’s the easiest way to get better in theory? Start by cheating! That is, if you can’t solve a problem in a few minutes, just look up the solution! Look it up, and copy it in your own notation. Of course, you’re not done: in a day or a week, try the problem again until you can do it on your own. Did you ‘memorize’ something? That wouldn’t be the worst thing in the world, but presumably you understand the steps well enough to repeat them. Fantastic, you’re an expert. On to the next problem.
In this bold spirit of outright cheating, I would like to first guide you through some of the most important and simplest ideas in non-equilibrium physics. As promised, before I ask any questions, here are the answers.
We will initially focus on two and three-state continuous-time systems described by simple ordinary differential equations (ODEs). These systems will let us understand the essentials of “relaxation phenomena” (are you impressed with my fancy phrase?) including their timescales and the relationship between transient behavior and steady-states, both equilibrium and non-equilibrium. Later, they will be a springboard to understanding discrete-time Markov state models (as explained in the answers, of course).
Consider a two-state system, with states A and B representing two configurational states of your system – protein, cell, solid material, whatever.
(1) ![]()
where ![]() is the reaction rate constant for the transition from A to B and likewise for
is the reaction rate constant for the transition from A to B and likewise for ![]() . We’ll describe the system by just two variables, the time-dependent populations of states A and B, denoted
. We’ll describe the system by just two variables, the time-dependent populations of states A and B, denoted ![]() and
and ![]() . The time-dependent behavior is then governed by these two ODEs:
. The time-dependent behavior is then governed by these two ODEs:
(2) 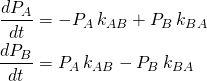
Your assignment is the following:
Write down the exact solution to the ODEs. Notice that I didn’t say to ‘solve’ the equations. You should just guess the solution. How? The basic picture is that the system relaxes exponentially from the initial state (i.e., your choices of the probabilities ![]() and
and ![]() ) to the final state which is equilibrium. Start with something you know. Do you know what equilibrium to expect? Hint: Think detailed balance. Do you know what time constant to expect in the exponential? Hint: It’s the simplest combination of the rate constants, but procedurally you can just denote it by some symbol and solve for it by differentiating your guess.
) to the final state which is equilibrium. Start with something you know. Do you know what equilibrium to expect? Hint: Think detailed balance. Do you know what time constant to expect in the exponential? Hint: It’s the simplest combination of the rate constants, but procedurally you can just denote it by some symbol and solve for it by differentiating your guess.
Stuck? Don’t panic – cheat! Check the answer!
Up next: what we can learn from the solutions.

