Remember our goal is to crawl before we walk. We want to absolutely master the basics, so that complicated systems are less incomprehensible. While it is essential to understand the two-state system, it’s not enough. Using three states will deepen our appreciation of relaxation phenomena and timescales. And we will take the first step toward understanding non-equilibrium steady states.

The discrete-state picture we continue to use is the simplest platform for analytical solutions. Deriving equations with explicit dependence on parameters (as opposed to numerical solutions for each choice of parameters) is a tried-and-true strategy of physics. Later we will connect the discrete-state picture to the underlying continuum physics.

Last time you were asked questions about the time-dependent solutions to the two-state problem, namely,

(1)   \begin{align*} P_A(t) &= P_A^\mathrm{eq} + \left[ P_A(0) - P_A^\mathrm{eq} \right] e^{-kt} \nonumber \\ P_B(t) &= P_B^\mathrm{eq} + \left[ P_B(0) - P_B^\mathrm{eq} \right] e^{-kt} \nonumber \end{align*}

where k = k_{AB} + k_{BA}.

Building on the available discussion, below are sketched answers to the questions from last post. I want to thank my group members – August George, John Russo, Barmak Mostofian, and Jeremy Copperman – for helping to clarify both the questions and answers.

  1. Why is the relaxation time 1/k governed by the rates in both directions?

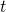    1. Once the probability in both states is non-zero (which will happen for any t>0), transitions occur in both directions … in turn affecting all time-dependent properties. Just thinking of the equations and noting that P_A(t) + P_B(t) = 1 for all t, we couldn’t have P_A depending on only one rate and P_B on the other.
  2. What is the rough meaning of the reciprocals of the rates?

    1. Since the (first-order) rate constants k_{AB} and k_{BA} are transition probabilities per unit time, their reciprocals represent the average time between transitions, also called the “dwell time” in the initial state.
  3. In qualitative terms, how can the solutions to the conformational A-B problem above help us understand binding kinetics? Hint: Consider the differences between binding and conformational ODEs.

    1. In the ODE description of binding, the association process is second-order, depending on the concentration (i.e., density \sim probability) of both receptor and ligand. If the concentration of, say, unbound receptor were somehow held constant by a chemostat, then the binding ODE could be mapped exactly onto the two-state ODEs we have been studying using an effective first-order rate constant (receptor concentration multiplied by on rate). Of course, that’s an un-natural condition, but roughly we can expect exponential-like relaxation from any non-equilibrium initial condition to equilibrium, if the total amount of ligand and receptor are maintained constant in the binding system.
  4. What assumptions are built into the two-state model? Equivalently, in what ways can a two-state model fail to describe the behavior of a complex system?

    1. There are three ways that I can think of. (i) Most obviously, complex systems could have many more than two states, which we’ll be exploring. (ii) The mass-action assumptions implicit in the ODEs are equivalent to an ideal-gas assumption of no interactions, and this can break down especially at higher concentrations. (iii) Because physical systems are continuous, it necessarily takes a finite amount of time for a transition to occur (even in a simple double-well system), whereas the ODE picture assumes instantaneous transitions.

Finally, the new homework. Consider a linear three-state system as sketched.

C:\Users\zuckermd\Box\physicalLens\htmlPhysicalLens\images\discreteThreeStateLinear.png

No direct transitions are allowed between states 1 and 3. Once again, all the answers are there for you.

  1. Write down the ODEs for this system.
  2. Solve for the equilibrium populations of this system.
  3. Sketch and write down the ODEs for a non-equilibrium steady state in which transition events from state 2 to 3 immediately generate feedback to state 1. That is, no transitions from 3 to 2 are allowed (so 3 can be called an absorbing state) and transitions from 2 to 3 effectively become transitions from 2 to 1 (though governed by the 2-to-3 rate constant).