To become stronger in theory, we do math. But we need to understand mathematical results in physical terms. The math and the conceptual picture must reinforce one another in our minds, or we’ll forget both. We also have to understand the assumptions underlying solvable models.

So it’s time for the solution to the previous problem … and new questions to understand that solution.

Last post, you were asked to solve the two-state system,

(1)   \begin{equation*} A \underset{k_{BA}}{\stackrel{k_{AB}}{\rightleftharpoons}} B \end{equation*}

where k_{AB} is the reaction rate constant for the transition from A to B and likewise for k_{BA}. States A and B represent two configurational states of a system like a protein, cell, solid material, or maybe a weather or epidemiological system. The time-dependent populations of states A and B, P_A(t) and P_B(t) are governed by

(2)   \begin{align*} \frac{ d P_A }{ dt } &= - P_A \, k_{AB} + P_B \, k_{BA} \nonumber \\ \frac{ d P_B }{ dt } &= P_A \, k_{AB}- P_B \, k_{BA} \end{align*}

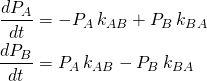
Hopefully, you have written down the solutions, which are

(3)   \begin{align*} P_A(t) &= P_A^\mathrm{eq} + \left[ P_A(0) - P_A^\mathrm{eq} \right] e^{-kt} \nonumber \\ P_B(t) &= P_B^\mathrm{eq} + \left[ P_B(0) - P_B^\mathrm{eq} \right] e^{-kt} \end{align*}

where k = k_{AB} + k_{BA}. You should be able to figure out the equilibrium fractions, P_A^\mathrm{eq} and P_B^\mathrm{eq}. As needed, a full discussion of this system is available.

Now that we know the math, the physics questions begin:

  1. Why is the relaxation time 1/k governed by the rates in both directions?
  2. What is the physical meaning of the reciprocals of the rates?
  3. In qualitative terms, how can the solutions to the conformational A-B problem above help us understand binding kinetics? Hint: Consider the differences between binding and conformational ODEs.
  4. What assumptions are built into the two-state model? Equivalently, in what ways can a two-state model fail to describe the behavior of a complex system?