Category: Statistical Uncertainty

Maximum Likelihood vs. Bayesian estimation of uncertainty

December 14, 2022 / dmz

When we want to estimate parameters from data (e.g., from binding, kinetics, or electrophysiology experiments), there are two tasks: (i) estimate the most likely values, and (ii) equally importantly, estimate the uncertainty in those values. After all, if the uncertainty is huge, it’s hard to say we really know the parameters. We also need to choose the model in the first place, which is an extremely important task, but that is beyond the scope of this discussion.
Continue reading

Let’s fix MD – You can help

February 13, 2020 / dmz

It’s my view that we must become statistical biophysicists. Why statistical? Because microscopic behaviors must be repeated zillions of times to create macroscopic effects. Can you help me shift the thinking in our community? See below for a collaboration opportunity.

Learn your lesson: Every method has its limits

July 12, 2019 / dmz

It was at breakfast during a recent conference that Prof. X leaned toward me and quietly said, “We tried using weighted ensemble but it didn’t work.” I got the sense he was trying not to broadcast this to other conference attendees, as a courtesy.

Are our “stories” fiction? Can we tell right from wrong?

February 27, 2019 / dmz

Here’s a true story from a number of years ago. A postdoc in the group comes to me in frustration. He has built a cool “semi-atomistic” coarse-grained protein model that has generated disappointing results. An alpha helix that’s clearly resolved in the X-ray structure of his protein completely unravels. Disappointment. But playing the optimistic supervisor, I ask, “Are we sure you’re wrong? Could that helix be marginally stable?” Further digging revealed an isoform of the protein where the helix in question was not resolvable via X-ray. Relief! I was pretty pleased with myself, I must say.

But now I’m disappointed that I was pleased.

Rules of Thumb for Sampling Assessment

January 29, 2019 / dmz

Some quick guidance for analyzing molecular dynamics (MD) or Markov-chain Monte Carlo (MC) data in hard-to-sample systems – e.g., biomolecules. I can summarize the advice this way: Ask not how to compute error bars. Ask first whether error bars are even appropriate. A meaningless error bar is more dangerous (to you and the community) than no error bar at all. This guidance is essentially abstracted from our recent Best Practices paper, and I hope it will set in context some of the theory discussed in an earlier post.

Absolutely the simplest introduction to Bayesian statistics

December 9, 2018 / dmz

I realized that I owe you something. In a prior post, I invoked some Bayesian ideas to contrast with boostrapping analysis of high-variance data. (More precisely, it was high log-variance data for which there was a problem, as described in our preprint.) But the Bayesian discussion in my earlier post was pretty quick. Although there are a number of good, brief introductions to Bayesian statistics, many get quite technical.

Here, I’d like to introduce Bayesian thinking in absolutely the simplest way possible. We want to understand the point of it, and get a better grip on those mysterious priors.

Recovering from bootstrap intoxication

June 13, 2018 / dmz

I want to talk again today about the essential topic of analyzing statistical uncertainty – i.e., making error bars – but I want to frame the discussion in terms of a larger theme: our community’s often insufficiently critical adoption of elegant and sophisticated ideas. I discussed this issue a bit previously in the context of PMF calculations. To save you the trouble of reading on, the technical problem to be addressed is statistical uncertainty for high-variance data with small(ish) sample sizes.

Let’s stop being sloppy about uncertainty

December 21, 2017 / twheeler

Let’s draw a line. Across the calendar, I mean. Let’s all pledge that from today on we’re going to give honest accounting of the uncertainty in our data. I mean ‘honest’ in the sense that if someone tried to reproduce our data in the future, their confidence interval and ours would overlap.

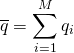There are a few conceptual issues to address up front. Let’s set up our discussion in terms of some variable $q$ which we measure in a molecular dynamics (MD) simulation at successive configurations: $q_0$ , $q_1$ , $q_2$ , and so on. Regardless of the length of our simulation, we can measure the average of all the values $\overline{q}= \displaystyle\sum_{i=1}^{M} q_i$ . We can also calculate the standard deviation σ of these values in the usual way as the square root of the variance. Both of these quantities will approach their “true” values (based on the simulation protocol) with enough sampling – with large enough $M$ .