So you know about molecular biophysics and want to think about cells. How should you get started? Let’s take the first few steps.
We’ll start with some concepts that should be familiar: coordinates and equilibrium vs. nonequilibrium behavior. We can frame our discussion by comparing something familiar, a protein, to a cell.
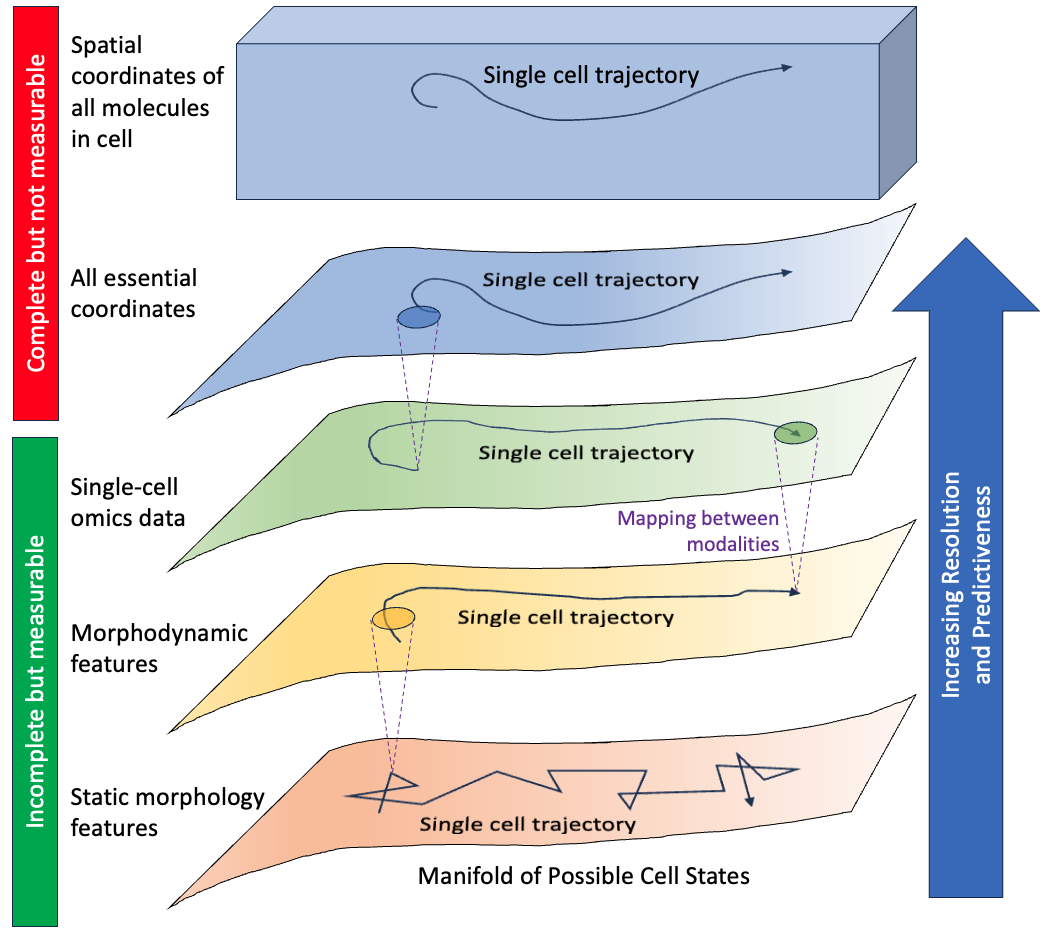
Conceptual hierarchy of descriptions of cell dynamics. Fundamentally, cells are described by spatial coordinates of all molecular components in atomic detail, so each full molecular configuration is a point in a high-dimensional hypervolume (top rectangular volume). Because of correlations among coordinates resulting from molecular interactions as well as the highly evolved and nonequilibrium nature of cell processes, a lower dimensional manifold of “essential” coordinates (uppermost curved surface) constitutes a full – but unmeasurable – description of instantaneous cell state sufficient to predict future behavior precisely. Any measurements of a cell will tend to exclude some essential information, leading to noisier representation of cell state and trajectories (curved arrows on manifolds). Some measurements will include more information than others, and a mapping can be generated even between descriptions at different resolutions (purple dashed lines), albeit with uncertainty – i.e., a range of possibilities – at the higher resolution. Also, a given measurement type can be augmented to be more descriptive and predictive: static morphology features can be measured over time to yield morphodynamic features, and morphodynamics can be augmented with genetically encoded protein labels (not shown). Conversely, noise in a given type of measurement reduces its predictiveness.
The obvious — and critical — difference from a protein is in the sheer number of coordinates required to fully characterize a cellular system. For a protein and its surrounding solvent, depending on the system at hand, the number of (x, y, z) coordinates might range from thousands to a million or so. Of course, a cell can have many copies of each protein and there are thousands of genes. This is not to mention the nucleic acids, lipids, carbohydrates, metabolites and signaling molecules floating around. To make a rough estimate, consider that a cell volume is ~10 μm3, which is equivalent to 1013Å3. Given that a typical chemical bond is a bit more than an angstrom, that means a cell has about a trillion atoms.
With such a staggering number of coordinates required to describe the instantaneous atomic configuration of a cell, we simply need to think differently. This is not to say the fundamental physics is any different: you can think of cells as vast molecular assemblies, and each molecule simply follows the laws of chemistry and physics as its dynamics unfold over time based on interactions with nearby molecules. In fact, some efforts have been made at simulating simplified cells, but molecular simulation is not a realistic possibility for true cellular timescales of minutes and hours.
The practical impossibility of characterizing the full set of cellular coordinates over meaningful lengths of time doesn’t mean we can’t think of a cell as executing the cell-scale version of molecular dynamics. We can and should imagine a cell follows a trajectory in a high dimensional hyper-volume: see figure.
As with a molecular system like a protein, however, the (x, y, z) positions of the cell’s atoms cannot take on arbitrary values because they are highly constrained and correlated. Steric repulsions occur and molecules exhibit both specific and non-specific affinities with one another so cell components are not going to be found in random places. The lipid bilayer is an extreme example: we don’t expect isolated lipids in the cytoplasm; instead, lipids will almost always be found next to other lipids.
So based on standard ideas of molecular biophysics, we know the effective dimensionality of a cell has to be much less than the 6N naïve phase-space count.
In my view, which is shared widely in the systems biology community, the molecular biophysics picture of correlations just presented will vastly over-count the dimensionality of functionally unique molecular configurations that typically occur in the cell, because the cell is not a simple bag of molecules. Rather, the cell is a highly evolved system that executes tremendously complex and orchestrated programs — e.g., signaling, biosynthesis, transcription — which are all highly driven nonequilibrium processes. (More on the nonequilibrium aspect in a moment.)
If we view the cell as a highly “programmed” molecular machine, it’s clear that true number of degrees of freedom characterizing a cell must be fairly low. Much closer to ten than to a trillion, in my opinion. This is another way of saying that a given cell can only exhibit a narrow range of behaviors. Epithelial cells will only do certain things, and macrophages other things. Sure there’s variation, but I believe it’s very constrained.
Another lens on the dimensionality of cell behavior can come from an analogy with the famous Levinthal paradox for protein folding. The idea for folding is that if the energy landscape in the unfolded state did not strongly favor folding, then a protein would spend its time transitioning among unfolded states, and thus folding would be a rare event on the timescales of living systems. Likewise, if cells were just randomly exploring all possible molecular configurations of all their constituents, then cells would not manage to do all that we know them to do.
Whereas protein folding can be a passive process (and this is what Levinthal was considering), the cell is a highly nonequilibrium thing. Almost every process is tightly controlled and driven. To give just one example, consider the post-translational modification of attaching a phosphate group to a protein, i.e., phosphorylation. Naively, we might say that every chemical reaction is reversible so the same enzyme that attaches the phosphate group should be the enzyme that removes it. But that is not so: kinases are not phosphatases. Separate enzymes catalyze the two reactions, and each involves different chemical species to ensure both steps are driven – but separately regulated. All this is to say that while there undoubtedly is stochasticity in a cell at the molecular scale, on average the cell is coordinating and driving behavior in according to a preset program.
I think of the cell as akin to a self-driving car on finite set of highways, rather than a drunken random walker. In my view, it’s an open question as to how stochastic cells really are. Some of our own recent work suggests that when cells are analyzed with an increasingly improved set of coordinates, the behavior looks less and less stochastic. A future post will explore characterization of cellular coordinates, which necessarily occurs based on incompletely informative and noisy coordinates (see figure).