Did you know that you can significantly change women’s performance on a challenging math test simply by providing a different explanation of the purpose of the test up front? And the same for Black students? Did you know there are ways to give advice and feedback that are demonstrated to improve performance in groups that suffer from (unconscious but inevitable) internalization of stereotypes? I learned these facts just a few weeks ago and find them astonishing. How can these crazy but simple things be true, and more importantly, why don’t most of us – professional scientists – know about them?
Author: dmz

Theory stronger, incrementally!! (Exercise 8)
The key lesson of all these exercises is that you can push yourself to be better and more confident in theory by tackling simple, paradigmatic problems in an incremental way. You must put pencil to paper! You must do it regularly. But once you do, the benefits come quickly. Each mini-realization builds into knowledge. Each solved simple problem builds your intuition for understanding complex systems.
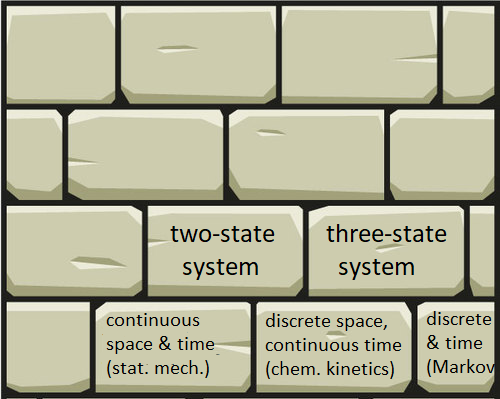
From continuous to discrete time (Exercise 7)
Give yourself a pat on the back if you’ve come this far. You have used simple exact solutions to differential equations to grasp the essentials of non-equilibrium processes. But there’s the physical process on the one hand, and the mathematical description on the other. We’ve used continuous-time math thus far. We now move to discrete time and get a taste for “Markov state models,” which implicitly employ time discretization in the field of biomolecular simulation.
Bring on the Context! (Exercise 6)
I think of knowledge like a house: it’s assembled from bricks that separately don’t do much. On its own, each brick is more prone to weathering. Likewise, each of our calculation bricks is easy to forget. We must learn to put these in context. We must always seek the connections to build a stronger house, which automatically preserves our individual bricks.
Squeezing more juice from three states (Exercise 5)
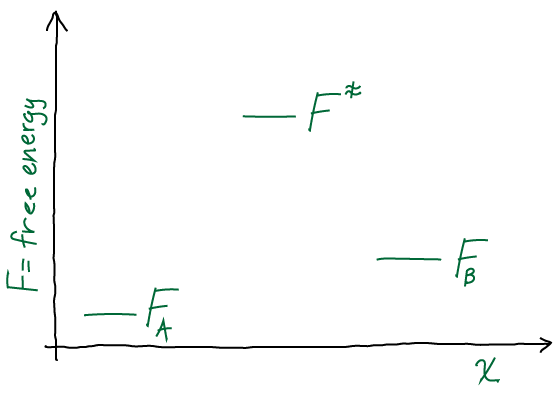
If the two-state system is the hydrogen atom, the three-state system is the hydrogen molecule. We have plenty more to learn about the three-state system. Mastering this material will really boost your confidence with non-equilibrium systems. Of course, we already studied the two-state system when it was out of equilibrium: remember the relaxation time ![]() ? But that was relaxation to equilibrium. Relaxation to a non-equilibrium steady state (NESS) is more interesting.
? But that was relaxation to equilibrium. Relaxation to a non-equilibrium steady state (NESS) is more interesting.

Relaxation and all that (Exercise 4)
Three states – now that is exciting! And I’m not kidding. You are poised to understand critical timescales in non-equilibrium statistical mechanics.

From two states to three (Exercise 3)
Remember our goal is to crawl before we walk. We want to absolutely master the basics, so that complicated systems are less incomprehensible. While it is essential to understand the two-state system, it’s not enough. Using three states will deepen our appreciation of relaxation phenomena and timescales. And we will take the first step toward understanding non-equilibrium steady states.

Squeezing physics from math (Exercise 2)
To become stronger in theory, we do math. But we need to understand mathematical results in physical terms. The math and the conceptual picture must reinforce one another in our minds, or we’ll forget both. We also have to understand the assumptions underlying solvable models.
So it’s time for the solution to the previous problem … and new questions to understand that solution.

Becoming theory-strong, at least stronger (Exercise 1)
With this post I want to begin a series of exercises designed to grow your strength in theory pertinent to statistical biophysics – i.e., in math, physics, theoretical chemistry. The goal is to help you find a sweet spot where you push yourself a little bit, and regularly so you can continue to improve. Along the way, you’ll (re)learn critical statistical physics, which will help you understand, implement, and assess methods and findings more effectively. Of course, you’re in!

Do we have a gender problem?
Ten days after I made this post, the New York Times published a related piece suggesting that one gender was more likely to up-sell their work with self-congratulatory description. (Guess which one?) This made me think more about the gender issue in our own field. Have something to say on this issue? Write me: zuckermd@ohsu.edu. I hope to do a post on this in the future, ideally relating the experiences of several individuals, anonymously if they wish. I will be at the Biophysics meeting in San Diego Monday and Tuesday if anyone wants to talk about it.
