“Proteins don’t know biology” is one of those things I’m overly fond of saying. Fortunately, it’s true, and it gives quantitative folks a foot in the door of the magical world of biology. And it’s not only proteins that are ignorant of their role in the life of a cell, the same goes for DNA, RNA, lipids, etc. None of these molecules knows anything. They can only follow physical laws.
Is this just a physicist’s arrogance along the lines of, “Chemistry is just a bunch of special cases, uninteresting consequences of quantum mechanics”? I hope not. To the contrary, you should try to see that cells employ basic physics, but of a different type than what we learned (most of us, anyway) in our physical sciences curricula. This cell biophysics is fascinating, not highly mathematical, and offers a way of understanding numerous phenomena in the cell, which are all ‘special cases’ … but special cases of what?
Hopefully, you’ve already gotten a basic sense of the cell’s business by reading Franklin Harold’s wonderful book, discussed in an earlier post. Harold makes explicit reference to the physical driving forces at play.
Here we’re going to take a peek at a book that makes the connection between physics and cell function more explicit, with a focus on the cell’s “molecular machines.” These macromolecular complexes perform incredible tasks like using stored free energy to pump a molecule of interest against its concentration gradient – e.g., importing nutrients into a cell or exporting toxins. Pumps can use free energy stored in the chemical potential difference of an ion on two sides of a cell membrane or using the free energy stored in ATP. Other machines perform even more dramatic feats such as “motors” which can change cell shape or contract muscle and the remarkable machinery which transcribes and translates DNA to RNA to protein along with error correction! Such topics are so incredible, they inspired me to write a second book, which is available online: Physical Lens on the Cell.
The book of interest now, which describes the fairly elementary physics needed to understand all this, is Terrell Hill’s Free Energy Transduction and Biochemical Cycle Kinetics. Perhaps this title is a little off-putting, but the book is absolutely a must-read.
Why do we want to know about cycles in the first place? Simply put, cycles are the main way a cell does its business at the molecular level. Think about one of the transporter machines I mentioned earlier, one that imports glucose into the cell. As with a human-scale machine, a molecular machine is something that needs to be used over and over. If the cell had to re-synthesize a new protein for every glucose molecule imported, that wouldn’t pay for itself. Instead, like in a factory, molecular machines are used repeatedly.
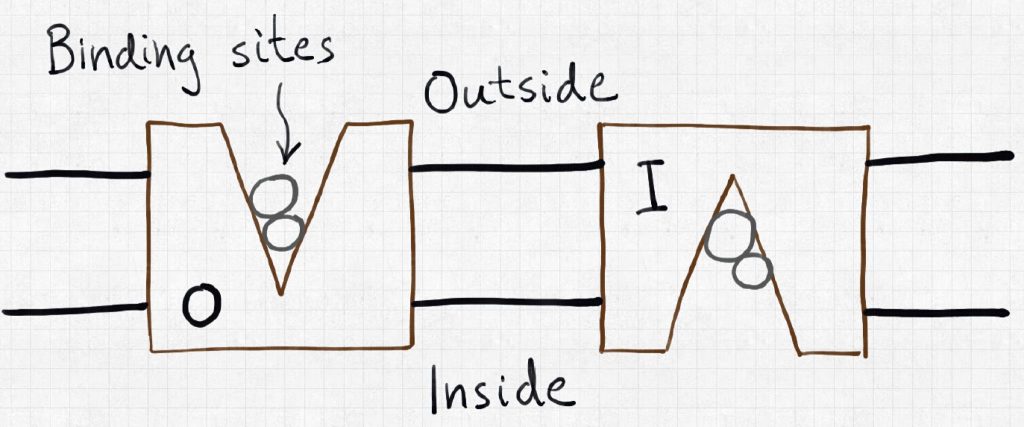
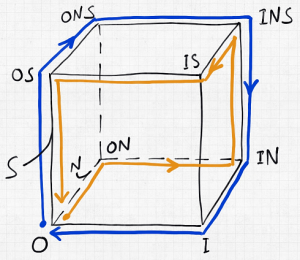
Let’s consider the simplest concrete example, sketched above, of a plasma-membrane bound transporter that can bind an ion (“N” – think sodium) a substrate (“S” – think sugar) in one of two conformations, outward-facing (“O”) and inward-facing (“I”). Outward-facing here means facing the exterior of a cell membrane, while inward-facing faces the cytoplasm or interior of the cell. This system has eight possible states, as shown in the cube diagram.
In the cube schematic, most of the (un)binding events are not shown explicitly, but are implicit: for example, from state OS to ONS, an ion N binds the outward-facing transporter (which already has substrate S bound); from IN to I, an ion unbinds from the inward-facing conformation.
Remarkably, this simple state space can describe transporters which lead to substrate import (from outside to inside, following the blue cycle) or to substrate export (from inside to outside, orange cycle). In fact, there are four possible cycles of each type! Can you find them? Each represents a possible process for a working machine. It’s a good bet that nature uses more than one of each kind.
Not only does Hill explain machine mechanisms using elegant diagrams similar to this one, but he covers the simple non-equilibrium physics underlying such cycles. The physics is non-equilibrium because it’s driven – in this case, by the lower chemical potential of N inside compared to outside. In equilibrium, there would be no net transport.
Hill teaches us how to think about non-equilibrium processes using elementary chemical kinetics, based on a simple mass action picture, and also how to quantify the corresponding free energies which arise from ideal gas/solution theory. In the case of our transporter, the free energy stored in the ion gradient must exceed the opposing substrate free energy difference in order for the processes to occur in the “forward” directions shown in blue and orange. (Blue and orange cycles would be found in entirely separate machines – it’s just that they’re shown in the same space.)
What’s remarkable, and obvious from the cube schematic, is that if the gradients are switched, these processes can be run in reverse. (Indeed, the molecular machines don’t “know” what they’re supposed to do, they can only follow the cycles allowed by their state spaces.) What’s more, the gradient of substrate could even be used to drive ion transport under the right conditions.
Pretty amazing stuff. So learn about these ideas, and how to quantify them, from Hill’s great book. It’s the perfect way to appreciate that simple physics can teach deep lessons about biology.
By the way, my advice is to focus on Hill’s first chapter. The second is largely devoted to technical methods which are cool, but much less valuable to a non-expert, in my view. (Caveat: Section 8 of Chapter 2 gives a nice discussion of the Hill relation connecting the rate and mean first-passage time.) The third and final chapter is quite interesting again, showing a more practical application of the theory to muscle contraction.
If you like what you read in Hill’s book, also check out my online book Physical Lens on the Cell, which goes into more detail on some of the issues and shows further applications of the ideas. But I want to be clear that 100% of the inspiration for my book comes from Hill.