Let’s draw a line. Across the calendar, I mean. Let’s all pledge that from today on we’re going to give honest accounting of the uncertainty in our data. I mean ‘honest’ in the sense that if someone tried to reproduce our data in the future, their confidence interval and ours would overlap.
There are a few conceptual issues to address up front. Let’s set up our discussion in terms of some variable ![]() which we measure in a molecular dynamics (MD) simulation at successive configurations:
which we measure in a molecular dynamics (MD) simulation at successive configurations: ![]() ,
, ![]() ,
, ![]() , and so on. Regardless of the length of our simulation, we can measure the average of all the values
, and so on. Regardless of the length of our simulation, we can measure the average of all the values 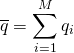 . We can also calculate the standard deviation σ of these values in the usual way as the square root of the variance. Both of these quantities will approach their “true” values (based on the simulation protocol) with enough sampling – with large enough
. We can also calculate the standard deviation σ of these values in the usual way as the square root of the variance. Both of these quantities will approach their “true” values (based on the simulation protocol) with enough sampling – with large enough ![]() .
.
The first key point to get straight is one that you probably know already: the difference between the natural scale of variation of the variable ![]() (see blue curve below, whose width is characterized by the standard deviation σ) and the uncertainty in the estimate of
(see blue curve below, whose width is characterized by the standard deviation σ) and the uncertainty in the estimate of ![]() (see red curve below). The standard deviation describes the range of values one expects to see in the list of
(see red curve below). The standard deviation describes the range of values one expects to see in the list of ![]() values, but the variability in the estimate of the mean can be much smaller – if there are many independent measurements.
values, but the variability in the estimate of the mean can be much smaller – if there are many independent measurements.
The uncertainty in ![]() is best framed in terms of a confidence interval. Understanding confidence intervals, which characterize statistical uncertainty, is essential and can be accomplished with a simple “thought experiment.” Imagine you repeat your simulation of length M many times, each time generating an average q (from the red distribution in the figure). If you consider the distribution of these
is best framed in terms of a confidence interval. Understanding confidence intervals, which characterize statistical uncertainty, is essential and can be accomplished with a simple “thought experiment.” Imagine you repeat your simulation of length M many times, each time generating an average q (from the red distribution in the figure). If you consider the distribution of these ![]() values there is a 90% chance that any future simulation (performed in an identical fashion, aside from stochasticity) will fall within the 5th and 95th percentiles of the
values there is a 90% chance that any future simulation (performed in an identical fashion, aside from stochasticity) will fall within the 5th and 95th percentiles of the ![]() distribution – regardless of whether all
distribution – regardless of whether all ![]() values are independent. This range of percentiles is the 90% confidence interval – even if we don’t know how to obtain them in practice.
values are independent. This range of percentiles is the 90% confidence interval – even if we don’t know how to obtain them in practice.
The confidence interval or another estimate of statistical uncertainty in principle can be smaller, even much smaller, than the standard deviation if the number of independent samples among the ![]() values is extremely large. That is, if a simulation is very long compared to system timescales, the estimate of an average from a single simulation should be very close to the “true” mean, based on infinite simulation, and the difference can be very small compared to σ. So, with more data, the red curve in the figure above would get narrower, as would the corresponding confidence interval.
values is extremely large. That is, if a simulation is very long compared to system timescales, the estimate of an average from a single simulation should be very close to the “true” mean, based on infinite simulation, and the difference can be very small compared to σ. So, with more data, the red curve in the figure above would get narrower, as would the corresponding confidence interval.
As you may know, a confidence interval can also be estimated based on the standard error of the mean (an estimator of the more official “standard uncertainty” noted in the VIM reference) but this assumes a symmetric Gaussian distribution of the variable and requires knowing the number of independent samples in your data. In MD simulation, only a small fraction of the frames generated may be independent. And it is a challenging if not impossible task to quantify this, as described below.
Error bars really only make sense when you’re sure multiple independent samples have been gathered. Without independent samples, we really have no way to understand the statistical uncertainty in our measurements.
In molecular simulation, we would want to know how many of the ‘zillions’ of trajectory frames are truly independent. Generally, this can be estimated by examining the autocorrelation time for the observable of interest (or implicitly via block-averaging) … with the risk that subtle correlations with slower processes may be masked by such an analysis. The transient “equilibration” time needed to relax the system initially also must be accounted for.
To examine sample size using a global correlation time (aka “decorrelation” time), Ed Lyman and I proposed examining trajectory frames at increasingly large time intervals. The data at each interval were compared to behavior expected for independent samples in order to infer the interval which led to quasi-independent behavior. This was a way to estimate an effective sample size for the whole system – i.e., the total simulation time divided by the minimum interval required for independence. The analysis can also show if the minimum interval is close to the overall simulation time, which would rule out good sampling.
How much of this is really relevant for the types of systems that usually are simulated?
If we’re honest, we’ll admit that for simulations of large and complex systems, we may never reach the timescales necessary to generate independent samples. What then? How do we even think about error in such cases?
To make things concrete, let’s assume we’ve run a one microsecond simulation of a system with a slow timescale of 10 μs. In this case, all of the trajectory frames are correlated. Of course, there’s nothing to stop us from calculating the standard deviation σ of any observable based on the trajectory, but we can expect that even the value of σ is highly biased – probably too small because we have not sampled important parts of the configuration space that require 10 μs to see. Certainly the standard error/uncertainty would be meaningless because there is not even one representative (independent) sample due to the short sampling time.
Well, there’s no getting around inadequate data, but statistical mechanics does have something to teach us here. We can view our single too-short trajectory, as in our prior thought experiment, as one sample of a distribution of 1 μs trajectories, all started from the same configuration. This is precisely the “initialized trajectory ensemble” discussed in an earlier post, which must obey a non-equilibrium Fokker-Planck equation. If we follow the ensemble of time-evolving trajectories, we can get the non-equilibrium configuration space distribution (ensemble) at any time point. This distribution will slowly relax toward equilibrium under typical conditions – or possibly to a non-equilibrium steady state under other constraints.
That conceptual picture is very powerful, but is it useful? Maybe or maybe not. If you just have the single too-short trajectory – sorry, you’re out of luck. However, if you have several too-short trajectories generated independently, then you can at least estimate the uncertainty in your observable of interest given the time elapsed and the initial state or initial distribution – call this an ensemble transient average. See the sketch below. For example, you could calculate the average of a quantity in each trajectory based on the interval from 95 – 100 ns. Then the multiple independent trajectories would enable you to estimate uncertainty in this explicitly transient quantity. It’s not an equilibrium estimate, but hey, it’s a genuine statistical mechanics observable that could also be measured by another group. Such an observable also might be compared among related systems (e.g., different ligands interacting with the same protein) in a statistically meaningful way.
If you want to learn more about uncertainty analysis – and figure out how to make meaningful error bars for your own data – consider looking at the article published in the “Living Journal of Computational Molecular Science,” a non-profit, community-run, low-cost, open-access venue for updateable articles oriented toward education and best practices. (Full disclosure: I helped to found the journal.) Feel free to look at the article and make suggestions directly on the article’s github page.
Further Reading
Chodera JD. “A simple method for automated equilibration detection in molecular simulations,” Journal of chemical theory and computation. 2016; 12(4):1799–1805.
Grossfield A, Patrone PN, Roe DR, Schultz AJ, Siderius DW, Zuckerman DM. “Best Practices for Quantification of Uncertainty and Sampling Quality in Molecular Simulations [Article v1. 0],” Living journal of computational molecular science. 2018;1(1).
Grossfield A, Zuckerman DM. “Quantifying uncertainty and sampling quality in biomolecular simulations,” Annu Rep Comput Chem. 2009. 5:23–48.
JCGM. JCGM 200: “International vocabulary of metrology – Basic and general concepts and associated terms (VIM)”. Joint Committee for Guides in Metrology; 2012.
Lyman E, Zuckerman DM. “On the Structural Convergence of Biomolecular Simulations by Determination of the Effective Sample Size,” J. Phys Chem B. 2007; 111(44):12876–12882.
Yang W, Bitetti-Putzer R, Karplus M. “Free energy simulations: Use of reverse cumulative averaging to determine the equilibrated region and the time required for convergence,” Journal of Chemical Physics. 2004; 120(6):2618–2628.
DM Zuckerman, Statistical Physics of Biomolecules: An Introduction, CRC Press, 2010.
[This post edited on Jan. 28, 2019 to reflect publication status of Grossfield et al.]


