This is yet another one of those things where, after reading this, you’re supposed to say, “Oh, that’s obvious.” And I admit it is kind of obvious … after you think about it for a few minutes! So spend those few minutes now to learn one more cool thing about non-equilibrium trajectory physics.
In non-equilibrium calculations of transition processes, we often wish to estimate a rate constant, which can be quantified as the inverse of the mean first-passage time (MFPT). That is, one way to define a rate constant is just reciprocal of the average time it takes for a transition. The Hill relation tells us that probability flow per second into a target state of interest (state “B”, defined by us) is exactly the inverse MFPT … so long as we measure that flow in the A-to-B steady state based on initializing trajectories outside state B according to some distribution (state “A”, defined by us) and we remove trajectories reaching state B and re-initialize them in A according to our chosen distribution.
Continue reading











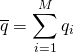 . We can also calculate the standard deviation σ of these values in the usual way as the square root of the variance. Both of these quantities will approach their “true” values (based on the simulation protocol) with enough sampling – with large enough
. We can also calculate the standard deviation σ of these values in the usual way as the square root of the variance. Both of these quantities will approach their “true” values (based on the simulation protocol) with enough sampling – with large enough